如何做证明：一种结构化的方法 [书籍]
How to Prove it: A Structured Approach [Book]

Highlights

• How to Prove It: A Structured Approach (by Daniel J. Velleman) 是一本旨在帮助学生从“如何求解”过渡到“如何证明”的书。顺便说一下，还有一本 1945 年的 How to Solve It: A New Aspect of Mathematics Method，作者是 Polya
• 本书先介绍了逻辑学和集合论的基本概念，以令读者熟悉并学会解读数学语言，因为一个证明通常是由多个基本结构组成的复杂结构。读者仅需具有高中水平的数学就可读懂本书
• 本文包含书中观点的截取或解读。本书的特点是例子多，每个例子都是为了说明一个重点而设的

Preface

许多学生第一次被要求做证明时会感到不知所措，因为他们在高中时所学的证明很可能只有几何学课堂上那种简单线性的思维。就像早期的编程，人们只是将命令一行行地往下列，直到后来“结构化编程”的出现。也就是说，命令具有了复杂的嵌套结构，比如在 while 循环中可以有 if else 条件判断，甚至另一个循环。做证明也是一样的。一个证明通常会结合多个基本结构。这也是本书书名的由来。

因为一个证明的结构取决于命题的逻辑形式，所以本书第一章和第二章分别介绍了逻辑连词和量词，以及集合论，以便于解释逻辑关系。第三章系统地阐述了结构化证明的技巧。第四章和第五章关于关系和函数，这是数学所有分支都会涉及到的基础概念。第六章关于数学推导，这个无论在数学还是计算机科学上都十分重要的证明方法。最后在第七章，前文所述的所有方法都会被整合在一起，来完成一些最难却最有意思的证明。

Introduction

数学的核心方法是 演绎推理（deductive reasoning） ：你需要通过现有的信息，推理出想知道的信息。而演绎推理在数学中通常以 证明（proof） 的形式呈现。接下来举几个例子，让你感受下证明是什么。看不太懂没关系，等你看完第三章就会明白了。

让我们来做一些关于质数的证明吧！回忆：质数是大于 1 的、不能被比它小的正整数整除的整数。但是在动手证明之前，我们要先知道该证明什么啊（就像读研）。因为许多灵感都来自于观察，所以我们可以先列出一些例子：

\[\begin{array}{ r l r l } n & \text{ Is } n \text{ prime? } & 2^n - 1 & \text{Is } 2^n - 1 \text{ prime? } \\ \hline 2 & \text{yes} & 3 & \text{yes} \\ 3 & \text{yes} & 7 & \text{yes} \\ 4 & \text{no: } 4 = 2 \cdot 2 & 15 & \text{no: } 15 = 3 \cdot 5 \\ 5 & \text{yes} & 31 & \text{yes} \\ 6 & \text{no: } 6 = 2 \cdot 3 & 63 & \text{no: } 63 = 7 \cdot 9 \\ 7 & \text{yes} & 127 & \text{yes} \\ 8 & \text{no: } 8 = 2 \cdot 4 & 255 & \text{no: } 255 = 15 \cdot 17 \\ 9 & \text{no: } 9 = 3 \cdot 3 & 511 & \text{no: } 511 = 7 \cdot 73 \\ 10 & \text{no: } 10 = 2 \cdot 5 & 1023 & \text{no: } 1023 = 31 \cdot 33 \\ \end{array}\]

通过观察上表，我们可以提出许多 猜想（conjecture），比如 ：

猜想 1 Suppose \(n\) is an integer larger than 1 and \(n\) is prime. Then \(2^n - 1\) is prime.

猜想 2 Suppose \(n\) is an integer larger than 1 and \(n\) is not prime. Then \(2^n - 1\) is not prime.

对于猜想 1，我们只需要继续填写列表就会发现：当 n 为 11 时，猜想错误。因此，11 是猜想 1 的一个 反例（counterexample）。确定“一个猜想是错误的”很容易，只需一个反例。但要确定“一个猜想是正确的”，只能通过 证明（prove）。

猜想 2 的证明 既然 \(n\) 不是质数，那么存在正整数 \(a\) 和 \(b\)，使得 \(a < n，b < n\)，且 \(n = ab\)。令 \(x = 2^b-1\) 且 \(y = 1 + 2^b + 2^{2b} + \cdots + 2^{(a-1)b}\)，则

\[\begin{align*} xy & = (2^b-1) \cdot (1 + 2^b + 2^{2b} + \cdots + 2^{(a-1)b}) \\ & = 2^b \cdot (1 + 2^b + 2^{2b} + \cdots + 2^{(a-1)b} ) - (1 + 2^b + 2^{2b} + \cdots + 2^{(a-1)b}) \\ & = (2^b + 2^{2b} + 2^{3b} + \cdots + 2^{ab}) - (1 + 2^b + 2^{2b} + \cdots + 2^{(a-1)b}) \\ & = 2^{ab} - 1 \\ & = 2^n - 1 \\ \end{align*}\]

由此可见，\(2^n - 1\) 总是可被写为两个更小的正整数 \(x\) 和 \(y\) 之乘积，所以 \(2^n - 1\) 不是质数，猜想 2 为真。

证毕

上面的证明的思路是寻找一个联系了前提和结论的数的形式，直接套用定义。

被证明为真的猜想就可以成为 定理（theorem） 了，即：

Theorem 1 如果 \(n\) 是一个大于 1 的整数且 \(n\) 是质数，那么 \(2^n - 1\) 是质数。

Theorem 2 如果 \(n\) 是一个大于 1 的整数且 \(n\) 不是质数，那么 \(2^n - 1\) 不是质数。

下面再看一个著名的证明，它是由欧几里德给出的：

Theorem 3 质数的个数是无穷的。

证明 假设质数的个数是有限的，并将所有的质数记为 \(p_1, p_2, \cdots , p_n\)。对于数 \(m = p_1p_2 \cdots p_n + 1\)，由于它大于 1，且不能被任何一个质数 \(p_i\) 整除（余数总是为 1 ），所以它应该是一个质数。但它却不在我们的有限质数列表里，产生矛盾。所以假设不成立，定理 3 得证。

证毕

上面的证明的思路是归谬法。

再来个长的，套路仍然是找形式套定义：

Theorem 4 对于每个正整数 \(n\)，总存在连续的 \(n\) 个不是质数的正整数。

证明 假设 \(n\) 是一个正整数，令 \(x = (n+1)!+2\)。如果 \(x, x+1, x+2, \cdots , x+(n-1)\) 都不是质数的话，定理就得证了。所以下面就来干这事：

如果把 \(x\) 的 2 提出来：

\[\begin{align*} x & = 1 \cdot 2 \cdot 3 \cdot 4 \cdots (n+1) + 2 \\ & = 2 \cdot (1 \cdot 3 \cdot 4 \cdots (n+1) + 1) \end{align*}\]

可见 \(x\) 可以被写为两个更小的正整数之乘积，所以 \(x\) 不是质数。同理可知，\(x + i \ (0 \leq i \leq n - 1)\) 也都不是质数：

\[\begin{align*} x + i & = 1 \cdot 2 \cdot 3 \cdot 4 \cdots (n+1) + (i+2) \\ & = (i+2) \cdot (1 \cdot 2 \cdot 3 \cdots (i+1) \cdot (i+3) \cdots (n+1) + 1) \end{align*}\]

证毕

1 Sentential Logic

1.1 Deductive Reasoning and Logical Connectives

Example 1.1.1 下面是一些演绎推理的例子，用以说明什么是“前提”，“结论”，以及一个论证是否“有效”：

1. 明天要么下雨要么下雪。
   明天太暖了不会下雪。
   因此，明天会下雨。

2. 要么男管家有罪，要么女仆有罪。
   要么女仆有罪，要么厨子有罪。
   因此，要么男管家有罪，要么厨子有罪。

在每个例子中，前两句话都是 前提（premises），最后一句话是 结论（conclusion）。只有当前提全为真能“迫使”结论也必为真时，这个论证才是 有效（valid） 的。因此，第一个论证是有效的，而第二个论证是无效的。注意，无论前提或结论在事实上是真是假，都不影响论证的有效性。即，论证的有效性只取决于论证的形式，与论证的内容无关。可将第一个论证抽象成以下形式：

P or Q.
not Q.
Therefore, P.

里面的一些连词，通常用以下符号来表示：

\[\begin{array}{cc} Symbol & Meaning \\ \hline \lor & \text{or (disjunction)} \\ \land & \text{and (conjunction)} \\ \lnot & \text{not (negation)} \\ \end{array}\]

Example 1.1.2 用上表的连词符号来表示以下命题的逻辑形式：

1. 要么 John 去趟商店，要么我们就没鸡蛋了。
2. Joe 打算离开家且再也不回来。
3. 要么 Bill 在干活而 Jane 闲着，要么 Jane 在干活而 Bill 闲着。

Solutions

1. \(P \lor Q\)，其中 P 表示“ John 去趟商店”，Q 表示“我们没鸡蛋”。
2. \(P \land Q\)，其中 P 表示“ Joe 打算离开家”，Q 表示 “ Joe 再也不回来”。
3. \((B \land \lnot J)\lor(\lnot B \land J)\)，其中 B 表示“ Bill 在干活”，J 表示“ Jane 在干活”。

Example 1.1.3 在上例中，我们已经学会将自然语言表示成逻辑符号的形式了。反过来，请将下列符号所表示的逻辑形式翻译成自然语言。注意，逻辑上的“与或非”，与自然语言中的“与或非”并不总是一致的。

1. \((\lnot S \land L)\lor S\)，其中 S 表示“ John is stupid”，L 表示“ John is lazy”。
2. \(\lnot S \land (L \lor S)\)，其中 S 和 L 的意义同上。
3. \(\lnot (S \land L) \lor S\)，其中 S 和 L 的意义同上。

Solutions

1. Either John isn’t stupid and he is lazy, or he’s stupid.
2. John isn’t stupid, and either he’s lazy or he’s stupid.
3. Either John isn’t both stupid and lazy, or John is stupid.

1.2 Truth Tables

通过真值表我们可以看到当前提为真时结论是否为真，即一个论证是否有效。如下面“与”、“或”、“非”的真值表。注意，我们的“或”允许 P 和 Q 同时为真。

\[\begin{array}{cccc} P & Q & P \land Q & P \lor Q \\ \hline F & F & F & F \\ F & T & F & T \\ T & F & F & T \\ T & T & T & T \\ \end{array} \quad \begin{array}{cc} P & \lnot P \\ \hline F & T \\ T & F \\ \end{array}\]

Example 1.2.1 下面我们来实践一下，为 \(\lnot (P \lor \lnot Q)\) 写出真值表。

Solution

\[\begin{array}{ccccc} P & Q & \lnot Q & P \lor \lnot Q & \lnot (P \lor \lnot Q) \\ \hline F & F & T & T & F \\ F & T & F & F & T \\ T & F & T & T & F \\ T & T & F & T & F \\ \end{array}\]

Example 1.2.2 遇到更复杂的式子，就该用更简洁的写法了。比如： \(\lnot (P \land Q) \lor \lnot R\)

Solution

麻烦的写法：

\[\begin{array}{ccccccc} P & Q & R & P \land Q & \lnot(P \land Q) & \lnot R & \lnot(P \land Q)\lor \lnot R \\ \hline F & F & F & F & T & T & T \\ F & F & T & F & T & F & T \\ F & T & F & F & T & T & T \\ F & T & T & F & T & F & T \\ T & F & F & F & T & T & T \\ T & F & T & F & T & F & T \\ T & T & F & T & F & T & T \\ T & T & T & T & F & F & F \\ \end{array}\]

简洁的写法：

\[\begin{array}{ c c } \text{Step 1} & \text{Step 2} \\ \begin{array}{ c c c } P & Q & \lnot (P \lor \lnot Q) \\ \hline F & F & \quad \textbf{F} \quad \quad \textbf{F} \\ F & T & \quad \textbf{F} \quad \quad \textbf{T} \\ T & F & \quad \textbf{T} \quad \quad \textbf{F} \\ T & T & \quad \textbf{T} \quad \quad \textbf{T} \\ \end{array} & \begin{array}{ c c c } P & Q & \lnot (P \lor \lnot Q) \\ \hline F & F & \quad F \quad \textbf{T}\ F \\ F & T & \quad F \quad \textbf{F}\ T \\ T & F & \quad T \quad \textbf{T}\ F \\ T & T & \quad T \quad \textbf{F}\ T \\ \end{array} \\ \text{Step 3} & \text{Step 4} \\ \begin{array}{ c c c } P & Q & \lnot (P \lor \lnot Q) \\ \hline F & F & \quad F\ \textbf{T}\ T\ F \\ F & T & \quad F\ \textbf{F}\ F\ T \\ T & F & \quad T\ \textbf{T}\ T\ F \\ T & T & \quad T\ \textbf{T}\ F\ T \\ \end{array} & \begin{array}{ c c c } P & Q & \lnot (P \lor \lnot Q) \\ \hline F & F & \textbf{F}\ F\ T\ T\ F \\ F & T & \textbf{T}\ F\ F\ F\ T \\ T & F & \textbf{F}\ T\ T\ T\ F \\ T & T & \textbf{F}\ T\ T\ F\ T \\ \end{array} \\ \end{array}\]

Example 1.2.3 前面一直在说用真值表可以判断一个论证是否有效，现在来看下怎么做。请判断以下论证是否有效：

1. Either John isn’t stupid and he is lazy, or he’s stupid.
   John is stupid.
   Therefore, John isn’t lazy.

2. The butler and the cook are not both innocent.
   Either the butler is lying or the cook is innocent.
   Therefore, the butler is either lying or guilty.

Solutions

1. 令 S 表示“John is stupid”，L 表示“John is lazy”，则论证的真值表为：

\[\begin{array}{cc:cc:c} & & \text{Premises} & & \text{Conclusion} \\ S & L & (\lnot S \land L) \lor S & S & \lnot L \\ \hline F & F & F & F & T \\ F & T & T & F & F \\ T & F & \textbf{T} & \textbf{T} & \textbf{T} \\ T & T & \textbf{T} & \textbf{T} & \textbf{F} \\ \end{array}\]

可见，当前提全为真时，结论既可为真也可为假。所以这个论证无效。

1. 令 B 表示为“The butler is innocent”，C 表示“The cook is innocent”，L 表示“The butler is lying”，则论证的真值表为：

\[\begin{array}{ccc:cc:c} & & & \text{Premises} & & \text{Conclusion} \\ B & C & L & \lnot(B \land C) & L \lor C & L \lor \lnot B \\ \hline F & F & F & T & F & T \\ F & F & T & \textbf{T} & \textbf{T} & \textbf{T} \\ F & T & F & \textbf{T} & \textbf{T} & \textbf{T} \\ F & T & T & \textbf{T} & \textbf{T} & \textbf{T} \\ T & F & F & T & F & F \\ T & F & T & \textbf{T} & \textbf{T} & \textbf{T} \\ T & T & F & F & T & F \\ T & T & T & F & T & T \\ \end{array}\]

可见，当前提全为真时，结论也全为真。所以这个论证有效。

Example 1.2.4 真值表不仅能够帮助判断一个论证是否有效，还能帮助判断两个命题是否等价。例如，判断以下式子是否等价：

\[\lnot(P \land Q), \quad \lnot P \land \lnot Q, \quad \lnot P \lor \lnot Q\]

Solution

列出各式的真值表，若无论前提如何，结论的真值都相同，则式子是等价的。

\[\begin{array}{ccccc} P & Q & \lnot(P \land Q) & \lnot P \land \lnot Q & \lnot P \lor \lnot Q \\ \hline F & F & T & T & T \\ F & T & T & F & T \\ T & F & T & F & T \\ T & T & F & F & F \\ \end{array}\]

可见，第一个式子和第三个式子是等价的。事实上，这被称为 DeMorgan’s laws。除此之外还有很多常用的 laws：

DeMorgan’s laws

\[\lnot (P \land Q) \text{ is equivalent to } \lnot P \lor \lnot Q. \\ \lnot (P \lor Q) \text{ is equivalent to } \lnot P \land \lnot Q.\]

Commutative laws

\[P \land Q \text{ is equivalent to } Q \land P. \\ P \lor Q \text{ is equivalent to } Q \lor P.\]

Associative laws

\[P \land (Q \land R) \text{ is equivalent to } (P \land Q) \land R. \\ P \lor (Q \lor R) \text{ is equivalent to } (P \lor Q) \lor R.\]

Idempotent laws

\[P \land P \text{ is equivalent to } P. \\ P \lor P \text{ is equivalent to } P.\]

Distributive laws

\[P \land (Q \lor R) \text{ is equivalent to } (P \land Q) \lor (P \land R). \\ P \lor (Q \land R) \text{ is equivalent to } (P \lor Q) \land (P \lor R).\]

Absorption laws

\[P \lor (P \land Q) \text{ is equivalent to } P. \\ P \land (P \lor Q) \text{ is equivalent to } P.\]

Double Negation law

\[\lnot \lnot P \text{ is equivalent to } P.\]

Example 1.2.5 上面的各种 laws 能帮助我们将看上去很复杂的命题简化成更容易懂的形式。例如，请简化以下式子：

1. \(\lnot(P \lor \lnot Q)\)
2. \(\lnot(Q \land \lnot P) \lor P\)

Solutions

\[\begin{array}{lrll} 1.\ \lnot(P \lor \lnot Q) \\ & \text{is equivalent to} & \lnot P \land \lnot \lnot Q & \text{(DeMorgan's law),} \\ & \text{which is equivalent to} & \lnot P \land Q & \text{(double negation law).} \\ \\ 2.\ \lnot(Q \land \lnot P) \lor P \\ & \text{is equivalent to} & (\lnot Q \lor \lnot \lnot P) \lor P & \text{(DeMorgan's law),} \\ & \text{which is equivalent to} & (\lnot Q \lor P) \lor P & \text{(double negation law),} \\ & \text{which is equivalent to} & \lnot Q \lor (P \lor P) & \text{(associative law),} \\ & \text{which is equivalent to} & \lnot Q \lor P & \text{(idempotent law),} \\ \end{array}\]

Example 1.2.6 我们把像 \(P \lor \lnot P\) 这样恒为真的命题叫 重言式（tautology），而像 \(P \land \lnot P\) 这样恒为假的命题叫 矛盾式（contradiction）。那么，以下的命题中，哪些是重言式，哪些是矛盾式？

\[P \lor (Q \lor \lnot P), \quad P \land \lnot(Q \lor \lnot Q), \quad P \lor \lnot(Q \lor \lnot Q)\]

Solution 首先对以上命题做张真值表：

\[\begin{array}{ccccc} P & Q & P \lor (Q \lor \lnot P) & P \land \lnot (Q \lor \lnot Q) & P \lor \lnot (Q \lor \lnot Q) \\ \hline F & F & T & F & F \\ F & T & T & F & F \\ T & F & T & F & T \\ T & T & T & F & T \\ \end{array}\]

可见，\(P \lor (Q \lor \lnot P)\) 是重言式，\(P \land \lnot(Q \lor \lnot Q)\) 是矛盾式。

再来一些关于重言式和矛盾式的 laws：

Tautology laws

\[P \land \text{(a tautology) is equivalent to } P. \\ P \lor \text{(a tautology) is a tautology. } \\ \lnot \text{(a tautology) is a contradiction. }\]

Contradiction laws

\[P \land \text{(a contradiction) is a contradiction. } \\ P \lor \text{(a contradiction) is equivalent to } P. \\ \lnot \text{(a contradiction) is a tautology.}\]

Example 1.2.7 练习运用以上 laws 来简化以下式子：

1. \(P \lor (Q \land \lnot P)\)
2. \(\lnot (P \lor (Q \land \lnot R))\land Q\)

Solutions

\[\begin{array}{lrll} 1.\ P \lor (Q \land \lnot P) \\ & \text{is equivalent to} & (P \lor Q) \land (P \lor \lnot P) & \text{(distributive law),} \\ & \text{which is equivalent to} & P \lor Q & \text{(tautology law)} \\ \\ 2.\ \lnot (P \lor (Q \land \lnot R)) \land Q \\ & \text{is equivalent to} & (\lnot P \land \lnot (Q \land \lnot R)) \land Q & \text{(DeMorgan's law),} \\ & \text{which is equivalent to} & (\lnot P \land (\lnot Q \lor \lnot \lnot R)) \land Q & \text{(DeMorgan's law),} \\ & \text{which is equivalent to} & (\lnot P \land(\lnot Q \lor R))\land Q & \text{(double negation law),} \\ & \text{which is equivalent to} & \lnot P \land ((\lnot Q \lor R) \land Q) & \text{(associative law),} \\ & \text{which is equivalent to} & \lnot P \land (Q \land (\lnot Q \lor R)) & \text{(commutative law),} \\ & \text{which is equivalent to} & \lnot P \land ((Q \land \lnot Q) \lor (Q \land R)) & \text{(distributive law),} \\ & \text{which is equivalent to} & \lnot P \land (Q \land R) & \text{(contradiction law).} \\ \end{array}\]

1.3 Variables and Sets

对于命题“2 is a prime number”我们可以用变量 \(x\) 来表示 2，因此命题就变成“\(x\) is a prime number”。我们甚至可以用一个字母来代表整个命题，比如 \(P(x)\) 是一个关于 \(x\) 的命题。

Example 1.3.1 分析以下命题的逻辑形式：

1. \(x\) is a prime number, and either \(y\) or \(z\) is divisible by \(x\).
2. \(x\) is a man and \(y\) is a woman and \(x\) likes \(y\), but \(y\) doesn’t like \(x\).

Solutions

1. \(P(x) \land (D(y,x) \lor D(z,x))\)
2. \(M(x)\land W(y) \land L(x,y) \land \lnot L(y,x)\)

因为之前的命题不含变量，要么为真要么为假，所以需要讨论的情况很简单。但是，当命题中含有变量时，命题的真假就取决于变量的取值了。例如 \(P(x)\) 表示“\(x\) is a prime number”，当 \(x=2\) 时，命题为真；当 \(x=4\) 时，命题却为假了。为了解决这个问题，我们需要引入 真值集合（truth set） 的概念。真值集合就是令“\(P(x)\) 为真”的 \(x\) 的取值集合，即：

\[\text{Truth set of } P(x) = \{x \mid P(x)\}.\]

接下来，回顾一下集合论的基本知识。集合（set） 里的东西叫 元素（element）。比如，集合 \(\{ 3,7,14 \}\) 的元素包括 3，7 和 14，元素的顺序可以为任意。注意，\(x \neq \{x\}\)，因为前者是一个元素，而后者是一个集合。\(7 \in A \) 表示“7 是此集合的一个元素”，\(11 \notin A \) 表示“11 不是此集合的元素”。如果显式地表示所有质数的集合，即“B = the set of all \(x\) such that \(x\) is a prime number”，则为：

\[B=\{x \mid x \text{ is a prime number }\}\]

其中，命题“\(x\) is a prime number”是集合的 元素测试（elementhood test）。要想知道某个东西是否为集合中的元素，只需要看它能不能令元素测试为真。

Example 1.3.2 用元素测试的形式重写以下集合：

1. \(E = \{2,4,6,8,\cdots\}\)
2. \(P = \{\text{George Washington, John Adams, Thomas Jefferson, James Madison,} \cdots\}\)

Solutions

1. \(E = \{n \mid n \text{ is a positive even integer}\}\)
2. \(P = \{z \mid z \text{ was a president of the United States}\}\)

在命题 \(y \in \{x \mid x^2 < 9\}\) 中，\(y\) 是一个 自由变量（free variable），表示此命题试图说明的东西，改变它的取值会改变命题的意思并影响它的真值。而 \(x\) 是一个 约束变量（bound variable），也可称为 虚变量（dummy variable） ，它只不过是为了便于我们表达意思而引入的变量，改变它的变量名并不影响命题的意思或真值。我们称 \(\{x \mid \cdots \}\) 约束（bind） 了变量 \(x\)。

注意：\(\{x \mid P(x)\}\) 只是个集合而不是命题，\(y \in \{x \mid P(x)\}\) 才是个命题，且它与 \(P(y)\) 是同一个意思。随着讲述的深入，清楚地区分“东西的表达式”和“命题的表达式”将变得越来越重要。

Example 1.3.3 以下命题是什么意思？每个命题中的自由变量是哪个？

1. \(a + b \notin \{x \mid x \text{ is an even number}\}\)
2. \(y \in \{x \mid x \text{ is devisible by } w\}\)
3. \(2 \in \{w \mid 6 \notin \{x \mid x \text{ is divisible by } w\}\}\)

Solutions

1. 意思：\(a+b\) 不是偶数。自由变量：\(a, b\)
2. 意思：\(y\) 能被 \(w\) 整除。自由变量：\(y, w\)
3. 意思：2 不能整除 6。没有自由变量，且命题为假

Example 1.3.5 还记得之前的“真值集合”的定义吧？请说出以下命题的真值集合：

1. Shakespeare wrote \(x\).
2. \(n\) is an even prime number.

Solutions

1. \(\{x \mid \text{Shakespeare wrote } x\} = \{ \text{Hamlet, Macbeth, Twelfth Night,} \cdots\}\)
2. \(\{n \mid n \text{ is an even prime number}\}\)

当命题包括自由变量时，我们通常会不自觉地根据上下文推断它是什么类型的东西，或者说是它的所有可能取值的全集，即，谈论域（universe of discourse）。比如：\(\mathbb{R} = \{x \mid x \text{ is a real number}\}\)。有时候，显式地写出谈论域会更好，比如将 \(\{x \mid x^2 < 9\}\) 写为 \(\{x \in \mathbb{R} \mid x^2 < 9\}\)。当自由变量的真值集合为整个谈论域时，命题是重言式。相反的，当自由变量的真值集合为空集 \(\emptyset\) 时，命题是矛盾式。

1.4 Operations on Sets

设 \(A\) 是命题 \(P(x)\) 的真值集合，\(B\) 是命题 \(Q(x)\) 的真值集合，那么 \(P(x) \land Q(x),\ P(x) \lor Q(x),\ \lnot P(x)\) 的真值集合是什么？

Definition 1.4.1

The intersection of two sets \(A\) and \(B\) is the set \(A \cap B\) defined as follows:

\[A \cap B =\{x \mid x \in A \text{ and } x \in B\}\]

The union of \(A\) and \(B\) is the set \(A \cup B\) defined as follows:

\[A \cup B =\{x \mid x \in A \text{ or } x \in B\}\]

The difference of \(A\) and \(B\) is the set \(A \setminus B\) defined as follows:

\[A \setminus B =\{x \mid x \in A \text{ and } x \notin B\}\]

Example 1.4.2 设 \(A = \{1,2,3,4,5\},\ B = \{2,4,6,8,10\}\)，请列出以下集合中的元素：

1. \(A \cap B\)
2. \(A \cup B\)
3. \(A \setminus B\)
4. \((A \cup B)\setminus(A \cap B)\)
5. \((A \setminus B)\cup(B \setminus A)\)

Solutions

1. \(\{2,4\}\)
2. \(\{1,2,3,4,5,6,8,10\}\)
3. \(\{1,3,5\}\)
4. \(\{1,3,5,6,8,10\}\)
5. \(\{1,3,5,6,8,10\}\)

Example 1.4.3 设 \(A = \{x \mid x \text{ is a man}\},\ B = \{x \mid x \text{ has brown hair}\}\)，问：\(A \cap B,\ A \cup B,\ A \setminus B\) 分别是什么？

Solution

\[A \cap B =\{x \mid x \text{ is a man and } x \text{ has brown hair}\} \\ A \cup B =\{x \mid \text{either } x \text{ is a man or } x \text{ has brown hair}\} \\ A \setminus B =\{x \mid x \text{ is a man and } x \text{ does not have brown hair}\}\]

我们可以利用 韦恩图（Venn diagrams） 来帮助我们直观地理解涉及三个集合以下的集合运算：

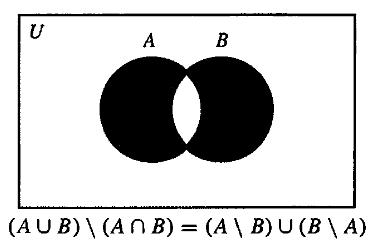
集合论中的 \(\cap \text{ , } \cup \text{ and } \setminus \) 可以分别和逻辑连接词 \(\land \text{ , } \lor \text{ and } \lnot\) 相对应。但是要注意，它们不是等价的：前者用于集合，后者用于命题。

\[\text{the truth set of } P(x) \land Q(x) = A \cup B \\ \text{the truth set of } P(x) \lor Q(x) = A \cap B \\ \text{the truth set of } \lnot P(x) = U \setminus A\]

Example 1.4.4 分析以下命题的逻辑结构：

1. \(x \in A \cap (B \cup C)\)
2. \(x \in A \setminus (B \cap C)\)
3. \(x \in (A \cap B) \cup (A \cap C)\)

Solutions

1. \(x \in A \land (x \in B \lor x \in C)\)
2. \(x \in A \land \lnot (x \in B \land x \in C)\)
3. \((x \in A \land x \in B) \lor (x \in A \land x \in C)\)

Definition 1.4.5 设 A 和 B 是集合。如果 A 的每个元素都同时是 B 的元素，那么 A 是 B 的 子集（subset），记作 \(A \subseteq B\)。如果 A 和 B 没有共同元素，即 \(A \cap B = \emptyset\)，则称 A 和 B 互斥（disjoint）。

Example 1.4.6 设 \(A = {\text{red, green}}, B = {\text{red, yellow, green, purple}} \text{ and } C = {\text{blue, purple}}\)。因为 A 的两个元素 red 和 green 均在 B 中，所以 \(A \subseteq B\)。因为 \(A \cap C = \emptyset\)，所以 A 和 C 互斥。

Theorem 1.4.7 对于任意集合 A 和 B，\( (A \cup B) \setminus B \subseteq A\)。

1.5 The Conditional and Biconditional Connectives

接下来介绍一个新的逻辑连接词：\(\to\)。我们用 \(P \to Q\) 来表示”If P then Q”。这种命题称为 条件命题（conditional statement），P 称为 前件（antecedent），Q 称为 后件（consequent）。

Example 1.5.1 分析以下命题的逻辑结构：

1. If it’s raining and I don’t have my umbrella, then I’ll get wet.

Solutions

1. \((R \land \lnot U) \to W\)
2. \((H \to \lnot C) \land (\lnot H \to B)\)

由以下真值表可得：

\[\begin{array}{cccccc} P & Q & P \to Q & \lnot P \lor Q & \lnot (P \land \lnot Q) & \lnot Q \to \lnot P\\ \hline F & F & T & T & T & T \\ F & T & T & T & T & T \\ T & F & F & F & F & F \\ T & T & T & T & T & T \end{array}\]

Conditional laws

\[P \to Q = \lnot P \lor Q = \lnot (P \land \lnot Q)\]

Contrapositive law

\[P \to Q \text{ is equivalent to } \lnot Q \to \lnot P\]

Example 1.5.2 以下命题，哪些是等价的？

1. If it’s either raining or snowing, then the game has been canceled.
2. If the game hasn’t been canceled, then it’s not raining and it’s not snowing.
3. If the game has been canceled, then it’s either raining or snowing.
4. If it’s raining then the game has been canceled, and if it’s snowing then the game has been canceled.
5. If it’s neither raining nor snowing, then the game hasn’t been canceled.

Solution

1. \((R \lor S) \to C\)
2. \(\lnot C \to (\lnot R \land \lnot S)\)，和命题 1 等价
3. \(C \to (R \lor S)\)
4. \((R \to C) \land (S \to C)\)，和命题 1 等价
5. \(\lnot (R \lor S) \to \lnot C\)

在数学中，\(P \to Q\) 通常还被表达为其他形式：

P implies Q.
Q, if P.
P only if Q.
P is a sufficient condition for Q.
Q is a necessary condition for P.

Example 1.5.3 分析以下命题的逻辑结构：

1. If at least ten people are there, then the lecture will be given.
2. The lecture will be given only if at least ten people are there.
3. The lecture will be given if at least ten people are there.
4. Having at least ten people there is a sufficient condition for the lecture being given.
5. Having at least ten people there is a necessary condition for the lecture being given.

Solutions

1. \(T \to L\)
2. \(L \to T\)
3. \(T \to L\)
4. \(T \to L\)
5. \(L \to T\)

在数学中，我们经常遇到 \(P \to Q\) 和 \(Q \to P\) 同时为真的情况。为了方便，我们引入一个新的连接词 \(\leftrightarrow\) 来表示 if and only if (iff)。而在现实中，我们说 if 时，经常实指的是 if and only if，它相当于 \((P \to Q) \land (\lnot P \to \lnot Q)\)。真值表如下：

\[\begin{array}{ccc} P & Q & P \leftrightarrow Q \\ \hline F & F & T \\ F & T & F \\ T & F & F \\ T & T & T \end{array}\]

Example 1.5.4 分析以下命题的逻辑结构：

1. The game will be canceled iff it’s either raining or snowing.
2. Having at least ten people there is a necessary and sufficient condition for the lecture being given.
3. If John went to the store then we have some eggs, and if he didn’t then we don’t.

Solutions

1. \(C \leftrightarrow (R \lor S)\)
2. \(T \leftrightarrow L\)
3. \(S \leftrightarrow E\)

2 Quantificational Logic

2.1 Quantifiers

我们已经知道，命题 P(x) 含有一个自由变量 x，当 x 取某些值时命题为真，而当 x 取另一些值时命题为假。有时我们会关心，有多少个取值能令 P(x) 为真。更具体地，我们想说“对于 x 所有可能的取值，命题 P(x) 都为真”，或者“至少存在一个 x 的取值，令命题 P(x) 为真”。因此，我们引进了两个新的符号来帮助我们表达这些意思。它们称为 量词（quantifiers）。

\(\forall x P(x)\) 的意思是：对于所有的 x，P(x)。\(\forall\) 是 全称量词（universal quantifier）。即，P(x) 的真值集合为 \(U\)。

\(\exists x P(x)\) 的意思是：存在一个 x，令 P(x)。\(\exists\) 是 存在量词（existential quantifier）。即，P(x) 的真值集合为 \(\emptyset\)。

Example 2.1.1 以下的式子什么意思？它们是真是假？

1. \(\forall x(x^2 \ge 0)\)，谈论域为 \(\mathbb{R}\)
2. \(\exists x(x^2-2x+3=0)\)，谈论域仍然为 \(\mathbb{R}\)
3. \(\exists x(M(x) \land B(x))\)，谈论域为所有人，M(x) 指 x is a man，B(x) 指 x has brown hair
4. \(\forall x(M(x) \to B(x))\)，谈论域和命题同上
5. \(\forall x L(x,y)\)，谈论域为所有人，L(x,y) 指 x likes y

Solutions

1. 对于所有的实数，\(x^2 \ge\)。真
2. 存在一个实数，\(x^2-2x+3=0\)。假
3. 存在一个棕色头发的男人。真
4. 对于所有人，如果他是男人，那么他一定是棕色头发的。假
5. 所有人都喜欢 y。只有当确定 y 是谁后，才能知道命题的真假。在此，y 影响了命题的真假，是自由变量；x 是约束变量

Example 2.1.2 分析以下命题的逻辑结构：

1. Someone didn’t do the homework
2. Everything in that store is either overpriced or poorly made
3. Nobody’s perfect
4. Susan likes everyone who dislikes Joe
5. \(A \subseteq B\)
6. \(A \cap B \subseteq B \setminus C\)

Solutions

1. \(\exists x \lnot H(x)\)
2. \(\forall x [S(x) \to (O(x) \lor P(x))]\)
3. \(\lnot \exists x P(x)\)
4. \(\forall x [\lnot L(x,Joe) \to L(Susan,x)]\)
5. \(\forall x (x \in A \to x \in B)\)
6. \(\forall x [(x \in A \land x \in B) \to (x \in B \land x \notin C)]\)

在描述关系时，显式地写出另一方会更好。例如，Some students are married. 我们可以简单地写成 \(\exists x (S(x) \land M(x))\)。更好的写法是 \(\exists x (S(x) \land \exists y M(x,y))\)，即 Some students are married to someone.

Example 2.1.3 分析以下命题的逻辑结构：

1. Everybody in the dorm has a roommate he doesn’t like
2. Nobody likes a sore loser
3. Anyone who has a friend who has the measles will have to be quarantined
4. If anyone in the dorm has a friend who has the measles, then everyone in the dorm will have to be quarantined
5. If \(A \subseteq B\), then \(A\) and \(C \setminus B\) and disjoint

Soluitons

1. \(\forall x [D(x) \to \exists y (D(y) \land \lnot L(x,y))]\)
2. \(\forall x (S(x) \to \lnot \exists y L(y,x))\)。这题有点脑筋急转弯，因为 a sore loser 并不指 a particular sore loser，而是指 all sore loser
3. \(\forall x [\exists y (F(x,y) \land M(y)) \to Q(x)]\)
4. \(\exists x [D(x) \land \exists y (F(x,y) \land M(y))] \to \forall z (D(z) \to Q(z))\)
5. \(\forall x (x \in A \to x \in B) \to \lnot \exists x (x \in A \land x \in C \land x \notin B)\)

当出现多个量词时，为了理清思路，最好每次一个、依次考虑。同时要注意，量词在命题中的前后顺序不可轻易改变，因为这可能会影响命题的意思和真假。

Example 2.1.4 以下命题是什么意思？它们是真是假？注：谈论域均为 \(\mathbb{N}\)，所有自然数的集合。

1. \(\forall x \exists y (x < y)\)
2. \(\exists y \forall x (x < y)\)
3. \(\exists x \forall y (x < y)\)
4. \(\forall y \exists x (x < y)\)
5. \(\exists x \exists y (x < y)\)
6. \(\forall x \forall y (x < y)\)

Solutions

1. 对于每一个自然数 x，都存在一个比它大的自然数 y。真
2. 存在一个自然数 y，使得所有的自然数都比它小。假
3. 存在一个自然数 x，使得所有的自然数都比它大。假
4. 对于每一个自然数 y，都存在一个比它小的自然数 x。假
5. 存在自然数 x 和 y，使得 x < y。真
6. 对于每一个自然数 x，它都比所有自然数小。假

2.2 Equivalences Involving quantifiers

Quantifier Negation laws

\[\lnot \exists x P(x) = \forall x \lnot P(x) \\ \lnot \forall x P(x) = \exists x \lnot P(x)\]

Example 2.2.1 否定这些命题，并将其重新表示成肯定式。

1. \(A \subseteq B\)
2. Everyone has a relative he doesn’t like

Solutions

1. \(\lnot A \subseteq B = \lnot \forall x (x \in A \to x \in B) = \exists x (x \in A \land x \notin B)\)
2. \(\lnot \forall x \exists y (R(x,y) \land \lnot L(x,y)) = \forall x \forall y (R(x,y) \to L(x,y))\)

注意，当我们谈论两个事物 x 和 y 时，我们并没有排除 x 和 y 是同一个东西的可能性。比如，“x 重婚了”的正确式子是 \(\exists y \exists z (M(x,y) \land M(x,z) \land y \neq z)\)。

Example 2.2.2 分析以下命题的逻辑形式：

1. All married couples have fights
2. Everyone likes at least two people
3. John likes exactly one person

Solutions

1. \(\forall x \forall y(M(x,y) \to F(x,y))\)
2. \(\forall x \exists y \exists z (L(x,y) \land L(x,z) \land y \neq z)\)
3. \(\exists x [L(John,x) \land \lnot \exists y (L(John,y) \land y \neq x)]\)

有时候，把谈论域显式地写出来会更清楚。比如没有约束变量的形式 \(\forall x \in \mathbb{R} P(x)\) 和有约束变量的形式 \(\forall x > 0 \exists y < 0 (y^2 = x)\)。

有约束变量的式子其实可以写成我们熟悉的无约束变量的形式。比如 \(\exists x \in A P(x) = \exists x (x \in A \land P(x))\)。

之前，我们都是依靠真值表来判断命题的真假。而这一招无法用在含有量词的命题上。怎么办呢？第三章再介绍。现在我们只需要记住：所有的数学命题结构都可以用我们已知的这些符号来表示（\(\land, \lor, \lnot, \to, \leftrightarrow, \forall, \exists\)）。这是很神奇很重要的一点。

Example 2.2.3 分析以下命题的逻辑结构：

1. 谈论域为自然数集 \(\mathbb{N}\)
   (a) x is a perfect square
   (b) x is a multiple of y
   (c) x is prime
   (d) x is the smallest number that is a multiple of both y and z
2. 谈论域为实数集 \(\mathbb{R}\)
   (a) The identity element for addition is 0
   (b) Every real number has an additive inverse
   (c) Negative numbers don’t have square roots
   (d) Every positive number has exactly two square roots

Solutions

1(a) \(\exists y (x = y^2)\)
1(b) \(\exists z (x = yz)\)
1(c) \(x > 1 \land \lnot \exists y \exists z (x = yz \land y < x \land z < x)\)
1(d) \(\exists a (x = ya) \land \exists b (x = zb) \land \lnot \exists w (w < x \land \exists c (w = yc) \land \exists d (w = zd))\)

2(a) \(\forall x (x + 0 = x)\)
2(b) \(\forall x \exists y (x + y = 0)\)
2(c) \(\forall x (x < 0 \to \lnot \exists y (y^2 = x))\)
2(d) \(\forall x (x > 0 \to \exists y \exists z (y^2 = x \land z^2 = x \land y \neq z \land \lnot \exists w (w^2 = x \land w \neq y \land w \neq z)))\)

2.3 More Operations on Sets

形如 \(P = \{ p_{i} \mid i \in I \}\) 的集合可称为 已索引族（indexed family），而 I 称为 索引集（index set）。其中，i 可以是包括数字的任何东西。

Example 2.3.1 分析以下命题的逻辑结构，写出所使用的集合论概念的定义。

1. \(y \in \{ \sqrt[3]{x} \mid x \in \mathbb{Q} \}\)
2. \( \{ x_{i} \mid i \in I \} \subseteq A\)
3. \( \{ n^2 \mid n \in \mathbb{N} \} \text{ and } \{ n^3 \mid n \in \mathbb{N} \} \text{ are not disjoint } \)

Solutions

1. \(\exists x \in \mathbb{Q} (y = \sqrt[3]{x})\)
2. \(\forall i \in I (x_{i} \in A)\)
3. \(\exists n \in \mathbb{N} \exists m \in \mathbb{N} (n^2 = m^3)\)

由于任何东西都可以成为集合中的元素，一个有趣而有用的想法是：将一个集合作为另一个集合的元素。比如 \(\mathcal{F} = \{ A, B, C \}\)，其中 \(A = \{ 1, 2, 3 \}, B = \{ 4 \}, C = \emptyset\)。因此，\(1 \in A, A \in \mathcal{F}, 1 \notin \mathcal{F}\)。

为了方便，我们经常会将一族集合定义为已索引族。比如 \(\mathcal{F} = \{ C_{s} \mid s \in S \}\)，其中 s 是某个学生，\(C_{s}\) 是该生的所有课程。一种重要的集合族是幂集：

Definition 2.3.2 设 A 是一个集合，则 A 的 幂集（power set） 是 A 的所有子集的集合，记作

\[\mathcal{P}(A) = \{x \mid x \subseteq A\}\]

Example 2.3.3 分析以下命题的逻辑结构。

1. \(x \in \mathcal{P}(A)\)
2. \(\mathcal{P}(A) \subseteq \mathcal{P}(B)\)
3. \(B \in \{ \mathcal{P}(A) \mid a \in \mathcal{F} \}\)
4. \(x \in \mathcal{P}(A \cap B)\)
5. \(x \in \mathcal(A) \cap \mathcal(B)\)

Solutions

1. \(\forall y (y \in x \to y \in A)\)
2. \(\forall x [\forall y (y \in x \to y \in A) \to \forall y (y \in x \to y \in B)]\)
3. \(\exists A \in \mathcal{F}\forall x (x \in B \leftrightarrow \forall y (y \in x \to y \in A))\)
4. \(\forall y (y \in x \to (y \in A \land y \in B))\)
5. \(\forall y (y \in x \to y \in A) \land \forall y (y \in x \to y \in B)\)

在分析一个复杂的命题时，一个很好用的原则是：从最外面的符号开始。

我们用 \(\cap \mathcal{F}\) 来表示这些集合共有的元素，用 \(\cup \mathcal{F}\) 来表示这些集合的元素的总体。

Example 2.3.4 令 \( \mathcal{F} = \{ \{ 1,2,3,4\}, \{2,3,4,5\}, \{3,4,5,6\} \}\)，写出 \(\cap \mathcal{F}, \cup \mathcal{F}\)。

Solution

\[\cap \mathcal{F} = \{3,4\} \\ \cup \mathcal{F} = \{1,2,3,4,5,6\}\]

Definition 2.3.5 设 \(\mathcal{F}\) 是一族集合，则它的交集和并集分别为：

\[\cap \mathcal{F} = \{x \mid \forall A \in \mathcal{F}(x \in A)\} = \{x \mid \forall A (A \in \mathcal{F} \to x \in A)\} (\mathcal{F} \neq \emptyset)\\ \cup \mathcal{F} = \{x \mid \exists a \in \mathcal{F}(x \in A)\} = \{x \mid \exists A (A \in \mathcal{F} \land x \in A)\}\]

Example 2.3.6 分析以下命题的逻辑形式。

1. \(x \in \cap \mathcal{F}\)
2. \(\cap \mathcal{F} \nsubseteq \cup \mathcal{G}\)
3. \(x \in \mathcal{P}(\cup \mathcal{F})\)
4. \(x \in \cup \{ \mathcal{P}(A) \mid A \in \mathcal{F} \} \)

Solutions

1. \(\forall A (A \in \mathcal{F} \to x \in A)\)
2. \(\exists x [\forall A \in \mathcal{F}(x \in A) \land \forall A \in \mathcal{G}(x \notin A)]\)
3. \(\forall A (y \in x \to \exists A \in \mathcal{F}(y \in A))\)
4. \(\exists A \in \mathcal{F} \forall y (y \in x \to y \in A)\)

将复杂的数学命题写为用逻辑符号表达的形式，能够帮助我们更好地判断命题的真假，比如当原形式比逻辑形式需要更多操作时。

对于已索引族集合，还可以用另一种方式来表示：设 \(\mathcal{F} = \{ A_{i} \mid i \in I \}\)，其中每个 \(A_{i}\) 是一个集合，则 \(\cap \mathcal{F}\) 指所有 \(A_{i}\) 共有的元素，\(\cap \mathcal{F} = \cap_{i \in I}A_{i} = \{ x \mid \forall i \in I (x \in A_{i})\}\)。

Example 2.3.7 设 \(I = \{1,2,3\}\)，对于每一个 \(i \in I\)，令 \(A_{i} = \{i, i+1, i+2, i+3\}\)。找出 \(\cap_{i \in I}A_{i}, \cup_{i \in I}A_{i}\)。

Solution

\[\cap_{i \in I} A_{i} = A_{1} \cap A_{2} \cap A_{3} = \{1,2,3,4\} \cap \{2,3,4,5\} \cap \{3,4,5,6\} = \{3,4\} \cup_{i \in I} A_{i} = \{1,2,3,4\} \cup \{2,3,4,5\} \cup \{3,4,5,6\} = \{1,2,3,4,5,6\}\]

Example 2.3.8 用 \(L(x,y)\) 表示“x likes y”，用 \(A(x,y)\) 表示“x admires y”。则对于每一个学生 s ，\(L_{s}\) 是 s 喜欢的所有学生的集合，\(A_{s}\) 是 s 欣赏的所有学生的集合。请描述以下集合：

1. \(\cap_{s \in S}L_{s}\)
2. \(\cup_{s \in S}L_{s}\)
3. \(\cup_{s \in S}L_{s} \setminus \cup_{s \in S}A_{s}\)
4. \(\cup_{s \in S}(L_{s} \setminus A_{s})\)
5. \((\cap_{s \in S}L_{s})\cap(\cap_{s \in S}A_{s})\)
6. \(\cap_{s \in S}(L_{s} \cap A_{s})\)
7. \(\cup_{b \in B}L_{b} \text{, where } B = \cap_{s \in S}A_{s}\)

3 Proofs

3.1 Proof Strategies

做证明就像玩拼图，你想怎么拼就怎么拼，没有任何规则。当然，在实际操作时，你不会每拼一块就留空一块、等到最后在来把洞填满，也不会从上到下、从左到右地严格按顺序拼。更可能的是，你先把四条边拼好，然后把一些容易完成的区域拼成大块儿，再把大块儿整合起来。有时候你会发现某些地方对不上，说明你犯了错误，需要退回重来。只有当拼图最后完成时对整个大局有了认识，你才知道，原来那条蓝线是湖边而不是天际。

数学家们通常用 定理（theorem） 的形式来表示一个数学问题的答案：如果这个定理的 假设（hypotheses） 是真的，那么某些结论一定是真的。通常，这些假设和结论中包含着自由变量，它们可以为谈论域中的任何元素。变量的一个取值称为 实例（instance）。只有对于定理的每一个实例来说，当假设为真其结论也为真时，定理才为真。哪怕仅存在一个实例，令假设为真时结论却为假，这个定理也是假的。这种实例称为 反例（counterexample）。

Example 3.1.1 考虑以下定理。

Theorem 如果 \(x > 3\) 且 \(y < 2\)，那么 \(x^2 - 2y > 5\)。

我们可以找到一个实例：x = 5 且 y = 1。可见对于这个实例来说，假设 x > 3 和 y < 2 是真的，结论 \(x^2 - 2y > 5\) 也是真的。在这里我们没有证明这个定理是正确的，我们只检查了一个实例，而证明定理正确需要检查所有的实例。

事实上，这个定理是正确的。如果我们把第二个假设去掉，则得到一个不正确的定理：

Incorrect Theorem 如果 \(x > 3\)，那么 \(x^2 - 2y > 5\)。

我们只需要找到一个反例，便可以判断定理不正确。比如当 x = 4 且 y = 6 时。

由此可见，找到一个反例便可以确定定理不正确，但确定定理正确的唯一方法是证明它。证明的第一条策略是：

若要证明一个形如 \(P \to Q\) 的结论，
先假设 P 为真，然后证明 Q 为真。

由于证明一个命题通常需要多次转换，我们把在某一时刻已知为真或被假设为真的命题称为 假定（given），把待证明的命题称为 目标（goal）。于是我们可以先利用假定完成目标的证明，然后再回头证明假定为真。

Example 3.1.2 设 a 和 b 是实数，证明：如果 \(0 < a < b\)，则 \(a^2 < b^2\)。

Scratch work

\[\begin{array}{cc} Givens & Goal \\ a \text{ and } b \text{ are real numbers} & (0 < a < b) \to (a^2 < b^2) \end{array}\]

根据上述证明技巧，我们可以将 0 < a < b 作为假定：

\[\begin{array}{cc} Givens & Goal \\ a \text{ and } b \text{ are real numbers} & a^2 < b^2 \\ 0 < a < b & \end{array}\]

可推得 \(a^2 < ab, ab < b^2, a^2 < ab < b^2\)。因此 \(a^2 < b^2\)。

Solution

Theorem Suppose a and b are real numbers. If 0 < a < b then a² < b².

Proof Suppose 0 < a < b. Multiplying the inequality a < b by the positive number a we can conclude that a² < ab < b², so a² < b², as required. Thus, if 0 < a < b then a² < b².

由此可见，想出证明方法的思考过程和证明过程是分开的。前者是心理，后者是数学。所以一开始看不懂证明是正常的。下面我们把刚才给出的证明策略重新呈现一遍：

To prove a goal of the form \(P \to Q\):
Assume P is true and then prove Q.

Scratch work

Before using strategy:

\[\]

(未完待续 to be continue)