机器学习中的神经网络 (3/3) [课程]
Neural Networks for Machine Learning (3/3) [Course]

All lectures
- Course information
- Lecture 1: Introduction
- Lecture 2: The Perceptron learning procedure
- Lecture 3: The backpropagation learning proccedure
- Lecture 4: Learning feature vectors for words
- Lecture 5: Object recognition with neural nets
- Lecture 6: Optimization: How to make the learning go faster
- Lecture 7: Recurrent neural networks
- Lecture 8: More recurrent neural networks
- Lecture 9: Ways to make neural networks generalize better
- Lecture 10: Combining multiple neural networks to improve generalization
- Lecture 11: Hopfield nets and Boltzmann machines
- Lecture 12: Restricted Boltzmann machines (RBMs)
- Lecture 13: Stacking RBMs to make Deep Belief Nets
- Lecture 14: Deep neural nets with generative pre-training
- Lecture 15: Modeling hierarchical structure with neural nets
- Lecture 16: Recent applications of deep neural nets
Lecture 11: Hopfield nets and Boltzmann machines
11.1 Hopfield Nets
回忆前文,没有隐藏神经元的对称 RNN 被称为“Hopfield Nets”。RNN 本来是很麻烦的东西,它可能维持在一个稳定状态,可能振荡,也可能处于混乱的难以预测的动态状态。但是 Hopfield 等人发现,如果你把 RNN 的神经元连接弄成对称的,那么无论初始状态如何,它都会走向一个能量最低的状态。用这个机制来实现记忆的想法非常诱人:在存储记忆的过程中,网络中的连接权重被确定下来。在提取记忆的时候,只要激活这个网络,让神经元按照一定的规则活动,则这个网络的最终状态总是能被重现。
我们规定,能量函数如图 Fig11.1-1A,它是由神经元活动以及每一对神经元之间的连接权重决定的。这个能量函数的神奇之处在于,对于某一个神经元,它的状态对总能量带来的影响仅与其附近的东西有关。即,我们很容易就能计算出,当这个神经元处于什么状态时,网络的总能量更低,然后我们就可以将神经元设为这个低能量状态。具体地说,神经元状态的影响仅仅取决于和它直接相连的神经元的状态及连接权重。当 energy gap < 0 时,该神经元的状态应设为 0;反之,则应设为 1(Fig11.1-1B)。
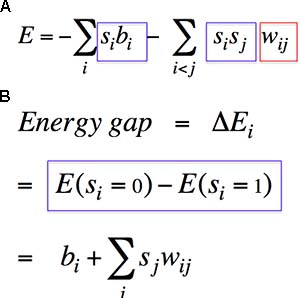
Fig11.1-1 The energy function (A) and the engergy gap (B) of Hopfield Nets.
Hopfield Nets 的更新步骤举例(假设 bias 为 0,如图Fig11.1-2):
- 随机初始化各神经元的状态
- 随机挑选一个神经元作为更新对象(红色问号,原状态为 0)
- 计算:energy gap = 1x(-4) + 0x3 + 0x3 = -4 < 0,所以状态应该保持不变(为0)
- 随机挑选另一个神经元,重复以上更新步骤,直到所有神经元都无法被改变
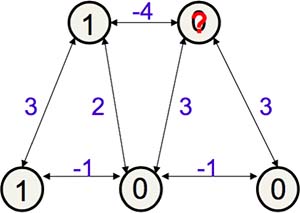
Fig11.1-2 How to update Hopfield Nets.
那么如何设计 Hopfield Nets,使得它的能量最低状态是我指定的样子呢?如果神经元状态是 -1 或 1,那么很简单,只需要令两个神经元之间的权重调整量等于二者乘积即可。如果神经元状态是 0 或 1,则会稍微复杂一些(Fig11.1-3)。

Fig11.1-3 How to set weights of Hopfield Nets.
然而,这样的 Hopfield Nets 最多只能有 0.15N 个记忆。在计算机系统里,这比存储权重所需的比特还少,似乎得不偿失。原因是,如果两个记忆在能量上离得很近,就会产生一个假能量低谷,也就是说,两个记忆产生了混淆(Fig11.1-4)。
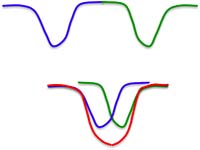
Fig11.1-4 Spurious minima in Hopfield Nets.
于是 Hopfield 等人又提出了一个策略:让网络从初始状态开始,自行变化,然后进行“去学习”。这样就能够弄掉假能量低谷,提高 Hopfield Nets 的存储能力。克里克(发现 DNA 结构的那个)等人甚至提出,这也许就是人为什么需要做梦!这令物理学家们十分着迷,此后有无数关于 Hopfield Nets 的研究发表在物理学杂志上。最后,Elizabeth Gardiner 找到了一种被统计学家称为“pseudo-likelihood”的方法,来充分开发 Hopfield Nets 的潜能。
11.2 Boltzmann Machines
前面说了,Hopfield Nets 没有隐藏神经元,且用于保存记忆。如果加上隐藏神经元,那么我们可以改变它的功能:用隐藏神经元的状态来解释输入。这就是 Boltzmann Machines。但是这带来了两个问题:如何防止网络陷入局部最低?如何学习权重?
如何防止网络陷入局部最低?如图 Fig11.2-1,由于网络总是往能量更低的地方走,所以网络一旦进入了局部低点 A 周围就出不来了,尽管 B 才是全局最低点。怎么办呢?首先,我们引入 Stochastic Binary Neurons,令每个神经元的状态不再为确定值,而根据概率来随机产生,概率大小不仅与周围的神经元状态和连接权重有关,还与“环境温度”有关。若温度极高,则状态 1 出现的概率约为 1/2;若温度为 0,则状态 1 概率约为 1。可见,“环境温度”控制了噪声的大小。温度越高,神经元越有可能跨过能垒,从 A 变为 B。随着温度慢慢下降,网络将稳定在全局最低点 B。这就是“模拟退火”方法。
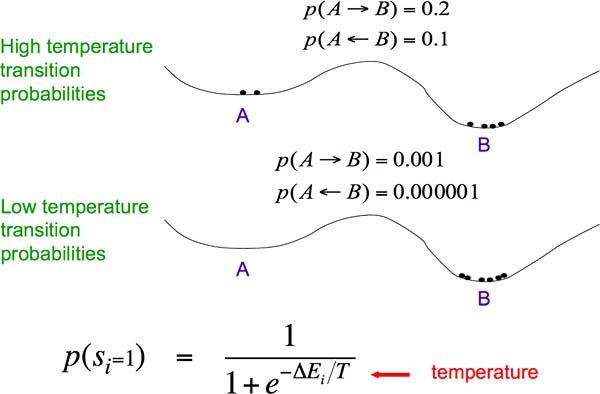
Fig11.2-1 Simulated annealing: adding noise to overcome the energy barrier.
事实上,Boltzmann Machines 之所以叫这个名字,就是因为网络状态出现的概率遵循 Boltzmann 分布。能量越低,出现的概率越大:
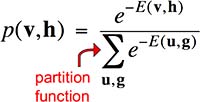
下一讲,我们将解决“如何学习权重”这个问题。
Lecture 12: Restricted Boltzmann machines (RBMs)
12.1 Boltzmann Machines 的学习算法
如何设置权重,使得在 Boltzmann Machine 中,目标输出(神经元状态)的能量最低,而其他状态的能量比较高?由于 Boltzmann Machines 属于无监督学习、没有目标输出,所以无法根据误差来调整权重。我们应该根据权重对目标输出出现的可能性的影响来调整权重,即把可能性对权重求得偏导作为权重调整量。然而神奇的是,这个偏导十分简单。它由两部分组成。第一部分是 positive phase:将输出神经元活动固定为一个目标输出,随机初始化其他神经元的活动,并让它们按规则变化至热平衡状态。“热平衡”不是指网络达到能量最低状态,而是指网络状态的分布不再变化。如此处理完所有训练样本后,统计该连接两端的神经元在热平衡状态时同时激活的频率。第二部分与第一部分相似,只是不固定输出神经元,让它们和其他神经元一样被随机初始化并达到热平衡状态。重复若干次后,统计出两个神经元同时激活的频率(negative phase)。也就是说,权重调整量与这两个频率之差相关(Fig12.1-1)。

Fig12.1-1 Learning of Boltzmann Machines.
直观地说,第一项相当于 Hopfield Nets 的学习过程,或 Hebbian 学习过程:若两个神经元在学习的过程中被同时激活,那么就增强二者之间的连接。而第二项相当于 Hopfield Nets 的去学习过程:若两个神经元在非学习过程中很容易被同时激活,那么这是一个假能量低谷,应该消除。
12.2 Restricted Boltzmann Machines
但是,如果按照上一节的方法来训练 Boltzmann Machines,将是一个非常低效的过程。因为如果网络很大,那么达到热平衡将是一个漫长的过程。而且,“是否真正达到了热平衡”这件事本身就难以判断。我们希望通过限制网络的连接度来降低学习的难度,于是就有了 Restricted Boltzmann Machines(RBM)。
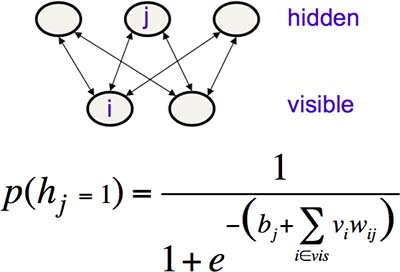
Fig12.2-1 Restricted Boltzmann Machines.
如上图 Fig12.2-1,RBM 只有一层隐藏神经元,且没有相互连接,每个隐藏神经元的状态概率可以通过上式直接计算出来,省却了漫长的热平衡之旅。另外一个提高学习效率的地方是,相较上文所述的“在 negative phase 令所有神经元随机初始化”,Tieleman 在 2008 年想到:先令输出神经元以目标输出来初始化,然后所有神经元按照规则并行地更新几次(不一定达到热平衡),顺序是“隐藏层、输出层、隐藏层”(一次 contrastive divergence),得到的输出神经元状态称为“幻象粒子”。最后在若干个幻象粒子中统计频率。权重的调整量为这个过程中产生的“训练数据”和“重建”之差。直观地,正如前文所说,因为“训练数据”应该成为网络能量最低的状态,所以应该增加这一项。而其他状态都不如训练数据的能量低,所以“重建”项应该被减去。这个方法在数学上没有很好的证明,却在实际应用中很有效(Fig12.2-2)。
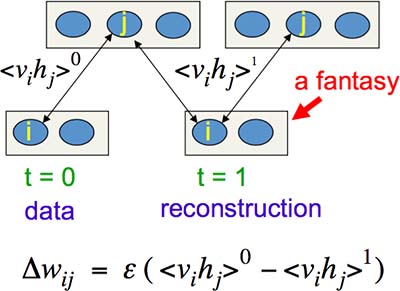
Fig12.2-2 Contrastive divergence for Restricted Boltzmann Machines.
下图 Fig12.2-3 是一个 RBM 例子:检测数字 2。在这个网络里,输出/输入神经元为 16x16 个,隐藏神经元为 50 个。可见,隐藏神经元检测到了不同的“2”的特征。

Fig12.2-3 Hidden neurons in a Restricted Boltzmann Machine to detect digit “2”.
Lecture 13: Stacking RBMs to make Deep Belief Nets
13.1 Backpropagation 的命运沉浮
Backpropagation 作为训练神经网络的核心算法,其实在 1970s 和 1980s 年代被独立开发出好几次。但是由于当时的计算机不够快,数据量也不够大,再加上支持向量机在简单任务上有更出色的表现,人们纷纷抛弃了神经网络。也就是说,神经网络的命运浮沉其实是由实现原因决定的,而非它的理论不完善。
在机器学习领域,有两派分支:统计学、人工智能。统计学对付的任务,通常维度低(少于100)、噪声大、特征简单,着力点在于将信号与噪声分离。而人工智能擅长的任务,通常维度高(多于100)、噪声影响不大、数据内在特征无法用简单的模型来表示,着力点在于表示出这种复杂的特征。
为什么说支持向量机不适合人工智能任务?本课的观点是,因为支持向量机只不过是 Perceptrons 的一种精巧变形,它无法应付高度抽象(多个隐藏层)的特征。
13.2 Belief Nets
但是 Backpropagation 也有局限。它要求数据有标签(“这是猫”、“这是狗”等),然而真实情况往往是,数据没有标签。当隐藏层很多时,学习所需的时间非常长。而且,大网络经常陷入局部最优解,而非全局最优解中。
我们可以通过将 Backpropagation 应用在非监督学习上,来绕过它的局限性:与其用它来直接执行任务,不如仅用它对数据进行预处理,提取特征。这一点在 Boltzmann Machines 上已经体现了。那么,我们应该用什么样的模型呢?是像 Boltzmann Machines 这样基于能量的模型?还是像最开始我们提到的因果型网络?或者二者的结合体?事实上,我们将要提到的 Belief Nets 是因果型网络。但是在此之前,让我们了解一下统计思维在人工智能领域中的浮浮沉沉。
人工智能的研究者曾在一段时间内都固执地认为神经元应该是确定的、“全或无”的,统计学方法在人工智能领域应该毫无用处。持有该想法的代表性人物是 MIT 的 AI 领军人物 Patrick Winston(没错,就是我之前推荐的这门课的教授)。人工智能领域的第一本教科书就是他于 1977 年写的,里面阐述了这种“反不确定性”的观点。然而如果我们阅读 John von Neumann 在 1958 的未竟手稿,他持的是相反意见,甚至提到了 Boltzmann。所以如果后者一直活着,也许人工智能领域的初期会是另一番景象:拥抱统计是主流。
幸好后来有人仍然将图形模型与统计模型结合了起来,并发现这样更奏效。从本质上说,图形模型表示了变量之间的依赖关系,而统计模型根据其他神经元的状态计算出某个神经元的状态。
Belief Nets 是一种类似于 RBM 的模型,它们都使用了 Stochastic Neurons。但是 RBM 是无向图(连接是对称的),而 Belief Nets 是有向图(连接是单向的)。RBM 的隐藏神经元之间没有连接,Belief Nets 可以有。而且 Belief Nets 的神经元状态更新算法与神经元个数呈指数关系,所以 Belief Nets 是稀疏网络(Fig13.2-1)。
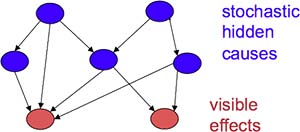
Fig13.2-1 Belief Nets.
13.3 The wake-sleep algorithm
(不很懂)